Compress your static word embedding without training

Apply Zipfian whitening for dimensional reduction. Compress embeddings to ~16% size with no training and minimal downstream loss.

TL;DR

• Use zipfian whitening to compress static word embeddings; it is fully training free yet stays strong.
• Experiments show 300d static word embedding compresses to 50d (~16%) with no STS score loss.
• Training-free baselines (random dimension drop, random projection, PCA/uniform whitening) fall as dims shrink; while Zipfian whitening stays strongest from 50d through 300d.

Rethinking dimensionality reduction on static word embeddings

Static word embeddings are having a small revival, as in Model2Vec and WordLlama. They are fast, cheap to serve, and easy to deploy compared to large transformer models, but they still eat RAM, so compression matters. Matryoshka representation learning is popular and strong, yet it requires contrastive training. A training-free approachHere “training-free” means no backprop; for example, a simple SVD-based method. would be easier to ship, but the default is still PCA. In this blog post, we show that using Zipfian Whitening to compress static word embeddings works very well.

Whitening (& PCA)

Before introducing Zipfian whitening, start with whitening, the baseline this note builds on. Say we have an embedding matrix with \(X \in \mathbb{R}^{V \times D}\) with rows \(x_w \in \mathbb{R}^{D}\) and we want compressed vectors \(z_w \in \mathbb{R}^{D'}\). Whitening here is PCA followed by scaling the retained components so they are uncorrelated and have unit variance. In this pipeline you center by the mean, form the covariance, eigendecompose, keep the top \(D'\) eigenpairs \(U_{D'}\) and \(S_{D'}\), and scale by the inverse square roots of those eigenvalues:

\(\begin{aligned} \mu &= {\color{#2475B0}{\frac{1}{V}}} \sum_w x_w \\ \Sigma &= {\color{#2475B0}{\frac{1}{V}}} \sum_w (x_w - \mu)(x_w - \mu)^\top \\ &= U S U^\top \quad (U_{D'}, S_{D'}) = \text{top-}D'\text{ eigenpairs} \\ W &= U_{D'} \operatorname{diag}\!\Big(\frac{1}{\sqrt{S_{D'} + \varepsilon}}\Big) \\ z_w^{\text{white}} &= W^\top (x_w - \mu) \end{aligned}\)

PCA-ed embedding is $$ \begin{aligned} z_w^{\text{PCA}} &= U_{D'}^\top (x_w - \mu) \end{aligned} $$

The issue is that both whitening and PCA above implicitly weight every word equally (\({\color{#2475B0}{1/V}}\)), ignoring token probabilities. High-frequency words tilt the covariance and drown out rare, informative ones.

Zipfian whitening

To fix the equal-weight issue, Zipfian Whitening keeps the same steps but considers word probabilities \(\color{#d33}{p(w)}\):

\[\begin{aligned} \mu_p &= \sum_w {\color{#d33}{p(w)}} x_w \\ \Sigma_p &= \sum_w {\color{#d33}{p(w)}}\, (x_w - \mu_p)(x_w - \mu_p)^\top \\ &= U S U^\top,\quad (U_{D'}, S_{D'}) = \text{top-}D'\text{ eigenpairs} \\ W_p &= U_{D'} \operatorname{diag}\!\Big(\frac{1}{\sqrt{S_{D'} + \varepsilon}}\Big) \\ z_w &= W_p^\top (x_w - \mu_p) \end{aligned}\]

The only change is swapping the uniform weight (\({\color{#2475B0}{1/V}}\)) for actual token probability \(\color{#d33}{p(w)}\) when taking expectations; this down-weights frequent words and preserves rare, informative ones. Compared with the original Zipfian whitening paper, the twist here is using it explicitly as a dimensionality-reduction method, like PCA.

You can plug in any \(\color{#d33}{p(w)}\) you like—estimated from a general corpus (e.g., Wikipedia) or from the target task. Task-specific \(\color{#d33}{p(w)}\) is usually stronger when you have enough text, acting as lightweight test-time adaptation.

Pseudocode

# Inputs: X[V, D] embeddings, p[V] frequencies (sum to 1), target dim D_out
# Output: Z[V, D_out] compressed + whitened embeddings
mu = p @ X                                 # weighted mean, since p sums to 1
Xc = X - mu
Sigma = (Xc.T @ np.diag(p) @ Xc) / p.sum()
U, S, _ = np.linalg.svd(Sigma)
U_d, S_d = U[:, :D_out], S[:D_out]
W = U_d @ np.diag(1.0 / np.sqrt(S_d + eps))
Z = Xc @ W

Experiments

Setup

We evaluate whether Zipfian whitening holds up when dimensions shrink.

• Base embeddings: fastText ja [https://huggingface.co/modern-static-embeddings/fasttext-ja-mecab].
• Task: STS tasks in JMTEB .
• Target dimensions: 10, 25, 50, 100, 150, 200, 300.
• Baselines: random dimension drop, random projection, PCA/uniform whitening.
• Ours: Zipfian whitening with Wikipedia \(p(w)\) and with STS \(p(w)\).

Results

STS across dimensions. Zipfian whitening with task p(w) tracks the original 300d accuracy even at 50d and stays strongest through 300d; generic p(w) also beats baselines.

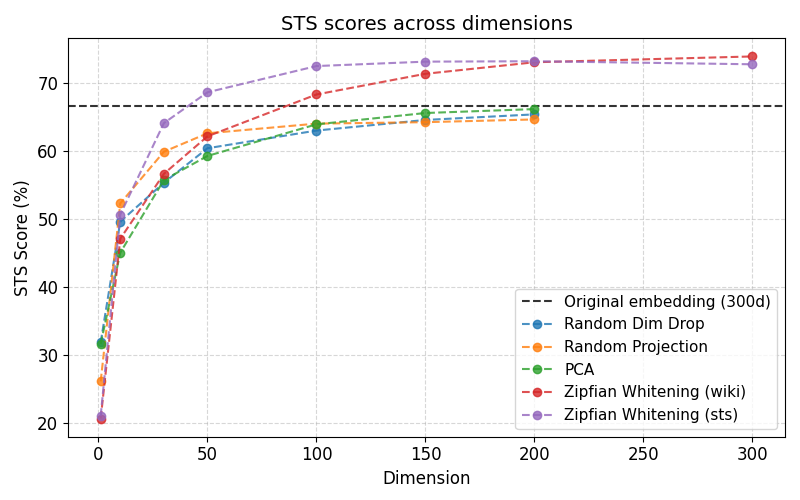
• Key observation: While baselines slide downward as dimensions shrink, Zipfian whitening (STS \(p\)) compresses 300d embeddings to 50d (~16%) with no STS score drop and stays best through the sweep.
• Zipfian whitening (STS \(p\)): hits the 300d reference line by 50d and stays on top through 300d.
• Zipfian whitening (wiki \(p\)): consistently above baselines, trailing task-specific \(p(w)\) by a small margin.
• Task \(p(w)\) > generic \(p(w)\) mirrors the importance of matching the test distribution.

Why it works

• Uniform whitening assumes all tokens carry equal information; Zipfian scaling rebalances by down-weighting high-frequency words and keeping rare, informative ones.
• Using task \(p(w)\) aligns the whitening step to the test distribution—an inexpensive form of test-time adaptation under covariate shift.

Conclusions

Using Zipfian whitening as a dimensionality-reduction method gives a training-free, frequency-aware drop-in for compressing static embeddings: swapping uniform weights for task-aware \(p(w)\) keeps STS accuracy even at 50d. Using task \(p(w)\) is the strongest option; a generic corpus still beats PCA/uniform whitening. If you have target text, compute \(p(w)\), whiten once, and ship smaller embeddings without retraining.

Acknowledgements

We thank Sho Yokoi, Yuji Yamamoto, and Hayato Tsukagoshi for discussions and insightful feedbacks.